Wurfbewegungen sind zusammengesetzte Bewegungen - es gilt das Superpositionsprinzip.
- eine gleichförmigen Bewegung in x-Richtung
- eine gleichmäßig beschleunigte/verzögerte Bewegung in y-Richtung
in Abhängigkeit von Fallbeschleunigung g und Luftwiderstand (freier Fall)
-
Senkrechter Wurf (Bewegungsrichtung und Fallrichtung sind parallel)
- Wurf nach oben: Körper wird von v0 mit g abgebremst, bis im oberen Punkt ve = 0 ist
- Wurf nach unten: Körper hat eine Anfangsgeschwindigkeit v0 und wird mit g beschleunigt
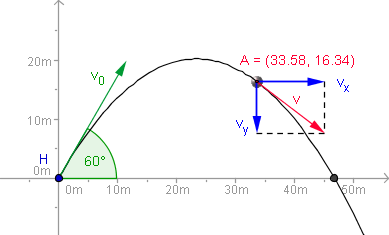
- Schräger/schiefer Wurf: zusammengesetzt aus senkrechter und waagerechter Wurfbewegung
Berechnungen zum schrägen Wurf:
Zur Berechnung vernachlässigen wir jegliche Reibungsvorgänge. Die Berechnung verläuft folgendermaßen:
-
Zuerst berechnen wir die Zeit, die der Körper bis zur maximalen Höhe benötigt:
Diese durch g gleichmäßig verzögerte Bewegung kann als rückwärts ablaufender freier Fall in y-Richtung betrachtet werden. Die Anfangsgeschwindigkeit $$v_0$$ ist betragsmäßig gleich der Endgeschwindigkeit $$v_{End}$$ - nur die Richtung ist entgegengesetzt.
Aus $$v_{End} = g \cdot t$$ wird $$t_1=\frac{v_{End}}{g}$$ und mit der y-Komponente der Anfangsgeschwindigkeit $$v_y = sin(\alpha) \cdot v_0$$ erhalten wir $$t_1=\frac{sin(\alpha) \cdot v_0}{g}$$.
-
Als Nächstes berechnen wir die maximale Höhe selbst:
Da wir den ersten Bewegungsabschnitt als rückwärts ablaufenden Freien Fall betrachten können, ist es so möglich zu ermitteln, aus welcher Höhe der Körper gefallen sein muss, um diese Endgeschwindigkeit (betragsmäßig gleich der Anfangsgeschwindigkeit) zu erhalten. Dabei verwenden wir als Formelzeichen für den Weg nicht s sondern h (Höhe), um Verwechslungen von x- und y-Richtung zu vermeiden.
In die s-t-Gleichung vom Freien Fall $$h=\frac{g}{2}\cdot t^2$$ setzen wir die Gleichung für t aus Schritt 1 ein: $$h=\frac{g}{2}\cdot \frac{{v_0}^2}{g^2}$$ und kürzen g.
Mit dieser Gleichung $$h=\frac{sin^2(\alpha) \cdot {v_0}^2}{2g}$$ erhalten wir die Höhe, die der Körper zusätzlich zu seiner eventuell vorhandenen Anfangshöhe erreicht.
-
Jetzt benötigen wir die Gesamtzeit des Wurfes - also vom Abwurf bis zum Aufschlag des Körpers. Hier kommt es auf die Abwurfhöhe an.
-
Hatte der Körper keine zusätzliche Abwurfhöhe, dauert der Vorgang insgesamt doppelt so lange wie der erste Abschnitt: $$t_{ges}= 2\cdot t_1$$.
-
Hatte der Körper aber eine zusätzliche Anfangshöhe, fällt er jetzt länger und weiter, als im Abschnitt 1. Er fällt jetzt aus der Gesamthöhe.
Wir müssen die Gleichung $$h=\frac{g}{2}\cdot t^2$$ nach t umstellen und die Gesamthöhe einsetzen: $$t_2 = \sqrt{\frac{2 \cdot h_{ges}}{g}}$$. Die Gesamtzeit ergibt sich dann aus der Summe von $$t_1$$ und $$t_2$$. Wer möchte, kann auch beide Gleichungen einsetzen, diese durch Quadrieren und Kürzen vereinfachen und so eine neue Gleichung für $$t_{ges}$$ aufstellen, um Folgefehler zu vermeiden.
-
-
Zum Schluss fehlt noch die Wurfweite. Da sich der Körper in x-Richtung mit konstanter Geschwindigkeit bewegt, verwenden wir das s-t-Gesetz der gleichförmigen Bewegung: $$s = v \cdot t$$.
Die Geschwindigkeit in x-Richtung erhalten wir mit dem Cosinus des Abwurfwinkels aus $$v_0$$ und die Gesamtzeit haben wir schon: $$s_w=cos(\alpha) \cdot v_0 \cdot t_{ges}$$